Camera localization with visual markers

When you work with autonomous vehicles, you usually dream with a small magic box that accurately tells you the position and attitude of the vehicle at all times. Because knowing where you are in the world is key to interact with the environment in an intelligent way. "But there's GPS!" —you might say—. Well, there is... Sometimes. When indoors, chances are low that you receive some GPS signal, unless you are close to a window or open door. Even outdoors, everybody has lost the route some time when driving in narrow streets with high buildings. Something that outsiders usually ignore is that, even if a GPS device is receiving the signal, the accuracy of the estimated position depends on many factors and it is bounded because of the nature of the system. So, the measure is not a single point in 3D space but a probability distribution. Your GPS device chooses the most probable point of that distribution. In fact, the usual error is in the range of meters or, if you are lucky, in the centimeter range. It is enough for some applications, like guiding a car driver, but, for some autonomous robotics applications, moving your robot half a meter further than you should could mean crashing with a wall. This is why GPS is not the solution to all problems.
In this project, I used Computer Vision to develop a localization method for robots using special landmarks in GPS-denied environments or where GPS does not give enough accuracy. Watch a video below —shot with an AR.Drone camera— with some results, and keep on reading this article if you want to better know what you watched.
Visual localization
There are motion capture systems that behave like a "local GPS". After installing several cameras around your workspace, they are able to detect and track small ball-shaped markers in 3D space. Cameras have strobe lights, either visible or infrared, that illuminate the reflective markers to detect them. If you stick some of these markers on your vehicle, your software can be informed of the vehicle pose at all times. I used one myself in the Australian Research Centre for Aerospace Automation (ARCAA) and it really makes things easy regarding autonomy. You have probably watched videos of quadrotors playing tennis at the ETH Zurich. Ever wondered how they do it? In fact, they have a Vicon motion capture system in their flying arena.
The drawbacks of motion capture systems are mainly two: they are expensive and they are static. If you manage to buy one and yout want to test your robots at different scenarios, you will have to spend a long time moving the hardware, mounting the cameras and setting the system up at every test location, provided that you get some power source, of course.
There are some folks that have used passive flat visual markers, like those used for Augmented Reality, for robot localization. If your mobile robot has a normal camera, which is usually the case, visual markers are a cheap and portable localization method. However, if your workspace is large or your camera resolution is low, you will need to produce big markers as well, so they can be seen by the robot from afar. Big flat markers can be cumbersome. If you place them flat on the ground, detection is rapidly lost by the robot because of perspective. If you set them vertically, they block the robot's field of view and offer high air resistance, which can lead to rupture because of wind when outdoors.
Monocular visual localization with 3D markers
At the time I developed this project, I was working in the Computer Vision Group, whose main research field was the control of autonomous vehicles using Computer Vision methods. We had several multirotor drones in the lab and we needed some kind of localization method, either for pure drone control or for experimental validation, but we did not have a motion capture system.
Because of our research activity, all the drones had an onboard camera. So, I decided to develop a marker-based monocular localization method with special markers that solved the problems of the traditional flat markers. The markers are shown in the picture below. They are cheap and easy to build, as the are made of PVC pipes covered with spray-painted foam. The black stripes are duct tape. On hard flat floors, a base made with wooden drawers is used to keep them vertical. When outdoors, the base can be removed and the pipes may be pinned in the soil.
Each pole is identified by a unique set of color stripes. Stripe colors can be those at the corners of the YUV space: orange, green, purple and light blue. Thus, for poles with three stripes, like the ones in the picture, a total of 43 = 64 unique identifiers can be generated. If the positions of the pole ends in the world frame are known, the system can determine the pose of the camera at all times, provided that at least two poles are seen.
In the video above you have watched the system working in real time on scenes with different lighting conditions. To show that the camera pose is actually estimated, some augmented reality elements are rendered on the video with OpenGL. The images were taken with an AR.Drone front camera, using the MAVwork framework, with a resolution of 320x240 pixels. At some frames, the poles are not detected and this is why there are some render glitches. The detection stage is the weakest part of the algorithm and I am working to make it more robust. However, the detection rate is still high enough for the application. Anyway, to overcome the detection problem, the output of this algorithm should be fused with the drone's odometry and a drone model using, for instance, a Kalman filter. That would allow for a continuous pose estimate without glitches. By the way, notice how the halos fly behind the poles. This is done by rendering the pole models on the stencil buffer.
How it works
In the end, that became part of my final thesis for the MS in Automatics and Robotics in which I was enrolled at that moment. If you need detailed information and you can read Spanish, the full thesis report is available here. Anyway, I will try below to summarize the basic concept.
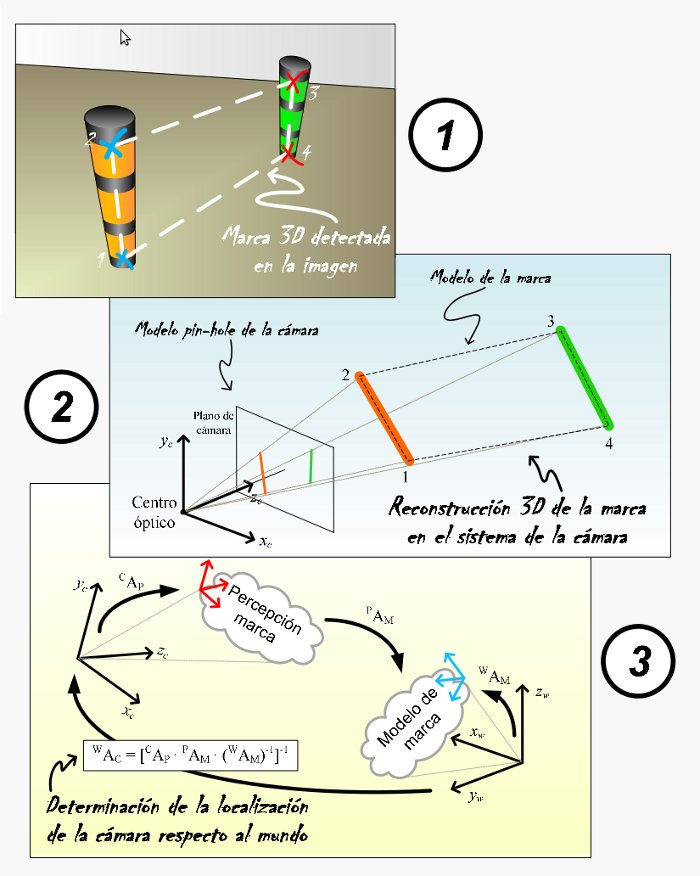
Camera localization algorithm steps
As seen in the diagram above, the camera localization algorithm basically performs three steps:
1) Detection of markers in the image
The first step consists in finding the markers in the camera images. The detection is performed in a cascade fashion. Simple detectors are run at every stage of the cascade. Each stage uses the output of the previous one, trying to detect more complex structures every time, from borders to full poles. The output is a set of 2D coordinates for all pole end points in the image. A group of poles with known geometry forms a marker.
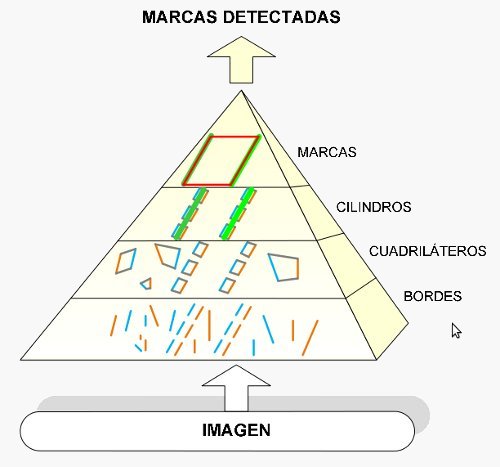
Mark detection in camera images is performed in a pyramidal or cascade fashion
2) 3D reconstruction of the markers in the camera space
With the marker known model, the camera model and the marker point projections on the camera plane, a system of non-linear equations can be built. The unknowns are the 3D coordinates of the marker points in the camera frame. A solution is found by transforming the system into a minimization problem and applying the Levenberg-Marquardt algorithm. This algorithm is initialized with an analitically found approximate solution that helps it converge to the correct solution. The output of this step is a set of 3D points in the camera frame corresponding to the 2D projections of step 1.
3) Camera pose estimation in the world frame
Once the reconstructed marker 3D points are found in the camera frame, it is easy to calculate the homogeneous transform to convert them into the corresponding marker model points in the world frame. From here, the camera pose in the world frame is obtained by simple linear algebra.